log: Difference between revisions

From Bohemia Interactive Community
Jump to navigation Jump to search
m (Text replacement - "<code>_([a-zA-Z0-9_]+) += +\[\[([a-zA-Z0-9_]+)\]\] +([0-9]+) *;?<\/code>" to "<sqf>_$1 = $2 $3;</sqf>")
m (Text replacement - "<code>([^ ]*)\[\[([a-zA-Z][a-zA-Z0-9_]+)\]\]([^ ]*)<\/code>" to "<code>$1$2$3</code>")
Line 34: Line 34:
|x1= <sqf>_log = log 10;</sqf>
|x1= <sqf>_log = log 10;</sqf>


|x2= <code>_log = [[log]] [[abs]] -10;</code>
|x2= <code>_log = log [[abs]] -10;</code>


|x3= <code>[[finite]] [[log]] -10; {{cc|Returns false}}</code>
|x3= <code>finite [[log]] -10; {{cc|Returns false}}</code>


|seealso= [[Math Commands]], {{Wikipedia|Logarithm|Logarithm}}
|seealso= [[Math Commands]], {{Wikipedia|Logarithm|Logarithm}}
Line 48: Line 48:
<dd class="note">
<dd class="note">
To clarify:
To clarify:
<code>y = 10 ^ x // x = [[log]] y</code>
<code>y = 10 ^ x // x = log y</code>
People use logarithm at the purpose of simplifying multiplication via exponents plus years before.
People use logarithm at the purpose of simplifying multiplication via exponents plus years before.
<code>23456*45634 = 1.07039e+009
<code>23456*45634 = 1.07039e+009

Revision as of 11:10, 12 May 2022

Logo A0.png1.00ofpe logo.png1.00Logo A1 black.png1.00Logo A2.png1.00A2 OA Logo.png1.50tkoh logo small.png1.00Arma 3 logo black.png0.50
Hover & click on the images for description

Description

Description:
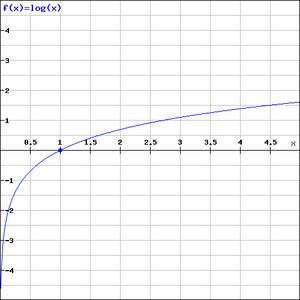
Base-10 logarithm of x.
The function of log(x) will never touch the y-axis.
Groups:
Math

Syntax

Syntax:
log x
Parameters:
x: Number - A positive number
Return Value:
Number

Examples

Example 1:
_log = log 10;
Example 2:
_log = log abs -10;
Example 3:
finite log -10; // Returns false

Additional Information

See also:
Math Commands, Logarithm

Notes

Report bugs on the Feedback Tracker and/or discuss them on the Arma Discord or on the Forums.
Only post proven facts here! Add Note
Posted on 23:14, 16 Jun 2014
ffur2007slx2_5
To clarify: y = 10 ^ x // x = log y People use logarithm at the purpose of simplifying multiplication via exponents plus years before. 23456*45634 = 1.07039e+009 log 23456 = 4.37025; log 45634 = 4.65929; (log 23456) + (log 45634) = 9.02954 10^((log 23456) + (log 45634)) = 10 ^ 9.02954 // same as 23456*45634 As modern usage, for instance, to evaluate another exponent when multiple is known (Which magnitude is 4 times stronger than 8.3 earthquake?): //_Unknown = log x; 8.3 = log y // x = 10 ^_Unknown; y = 10 ^8.3 //x/y = (10 ^_Unknown)/(10 ^8.3) = log 4 // x/y = _Unknown – 8.3 = 0.6 //_result = 8.9 magnitude _result = (log 4) + 8.3
Retrieved from "https://community.bistudio.com/wiki?title=log&oldid=312524"