vectorCrossProduct: Difference between revisions
m (format) |
m (template:command argument fix) |
||
| Line 9: | Line 9: | ||
| Cross product of two 3D vectors. | | Cross product of two 3D vectors. | ||
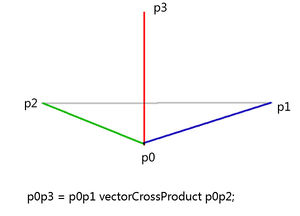
<br>In layman's terms, if you have a polygon (surface) defined by 3 points, you can find a normal to it (just like terrain [[surfaceNormal]]). To invert direction of the normal, swap arguments around. |= | <br>In layman's terms, if you have a polygon (surface) defined by 3 points, you can find a normal to it (just like terrain [[surfaceNormal]]). To invert direction of the normal, swap arguments around. |DESCRIPTION= | ||
____________________________________________________________________________________________ | ____________________________________________________________________________________________ | ||
| vector1 '''vectorCrossProduct''' vector2 |= | | vector1 '''vectorCrossProduct''' vector2 |SYNTAX= | ||
|p1= vector1: [[Array]] - in form [x, y, z] |= | |p1= vector1: [[Array]] - in form [x, y, z] |PARAMETER1= | ||
|p2= vector2: [[Array]] - in form [x, y, z] |= | |p2= vector2: [[Array]] - in form [x, y, z] |PARAMETER2= | ||
| [[Array]] - vector [x, y, z] | | [[Array]] - vector [x, y, z] | ||
<br><br> | <br><br> | ||
[[Image:crossProduct.jpg|300px]]|= | [[Image:crossProduct.jpg|300px]]|RETURNVALUE= | ||
____________________________________________________________________________________________ | ____________________________________________________________________________________________ | ||
|x1= <code>_vector = [1,1,1] [[vectorCrossProduct]] [2,2,2];</code> |= | |x1= <code>_vector = [1,1,1] [[vectorCrossProduct]] [2,2,2];</code> |EXAMPLE1= | ||
|x2= <code>_vectorUp = [0,1,0] [[vectorCrossProduct]] [-1,0,0]; //[0,-0,1]</code> |= | |x2= <code>_vectorUp = [0,1,0] [[vectorCrossProduct]] [-1,0,0]; //[0,-0,1]</code> |EXAMPLE2= | ||
|x3= <code>_vectorSide = ([[vectorDir]] [[player]]) [[vectorCrossProduct]] ([[vectorUp]] [[player]]);</code> |= | |x3= <code>_vectorSide = ([[vectorDir]] [[player]]) [[vectorCrossProduct]] ([[vectorUp]] [[player]]);</code> |EXAMPLE3= | ||
____________________________________________________________________________________________ | ____________________________________________________________________________________________ | ||
| [[vectorAdd]], [[vectorDiff]], [[vectorDotProduct]], [[vectorCos]], [[vectorMagnitude]], [[vectorMagnitudeSqr]], [[vectorMultiply]], [[vectorDistance]], [[vectorDistanceSqr]], [[vectorDir]], [[vectorUp]], [[setVectorDir]], [[setVectorUp]], [[setVectorDirAndUp]], [[vectorNormalized]], [[vectorFromTo]] |= | | [[vectorAdd]], [[vectorDiff]], [[vectorDotProduct]], [[vectorCos]], [[vectorMagnitude]], [[vectorMagnitudeSqr]], [[vectorMultiply]], [[vectorDistance]], [[vectorDistanceSqr]], [[vectorDir]], [[vectorUp]], [[setVectorDir]], [[setVectorUp]], [[setVectorDirAndUp]], [[vectorNormalized]], [[vectorFromTo]] |SEEALSO= | ||
}} | }} | ||
Revision as of 14:51, 7 April 2019
Description
- Description:
- Cross product of two 3D vectors.
In layman's terms, if you have a polygon (surface) defined by 3 points, you can find a normal to it (just like terrain surfaceNormal). To invert direction of the normal, swap arguments around. - Groups:
- Uncategorised
Syntax
- Syntax:
- vector1 vectorCrossProduct vector2
- Parameters:
- vector1: Array - in form [x, y, z]
- vector2: Array - in form [x, y, z]
- Return Value:
- Array - vector [x, y, z]
Examples
- Example 1:
_vector = [1,1,1] vectorCrossProduct [2,2,2];- Example 2:
_vectorUp = [0,1,0] vectorCrossProduct [-1,0,0]; //[0,-0,1]- Example 3:
_vectorSide = (vectorDir player) vectorCrossProduct (vectorUp player);
Additional Information
- See also:
- vectorAddvectorDiffvectorDotProductvectorCosvectorMagnitudevectorMagnitudeSqrvectorMultiplyvectorDistancevectorDistanceSqrvectorDirvectorUpsetVectorDirsetVectorUpsetVectorDirAndUpvectorNormalizedvectorFromTo
Notes
-
Report bugs on the Feedback Tracker and/or discuss them on the Arma Discord.
Only post proven facts here! Add Note
Notes
- Posted on 28 Jun, 2014
- ffur2007slx2_5
-
(ArmA3 1.22)Algorithm:
Vector1 = [x1,y1,z1]; Vector2 = [x2,y2,z2]; Result = [(y1 * z2) – (z1 * y2),(z1 * x2) – (x1 * z2),(x1 * y2) – (y1 * x2)];It is recommended to use vectorCrossProduct instead of BIS_fnc_crossProduct.
